线段树

Posted on Views:

线段树

基础知识

以查询区间最大值为例：
由分治的思想可知：区间 \([L,R]\) 的最大值等于 \(\max([L, M], [M + 1, R])\)
在区间 \([1,n]\) 上建线段树，以区间 \([1, 10]\) 为例，如图：

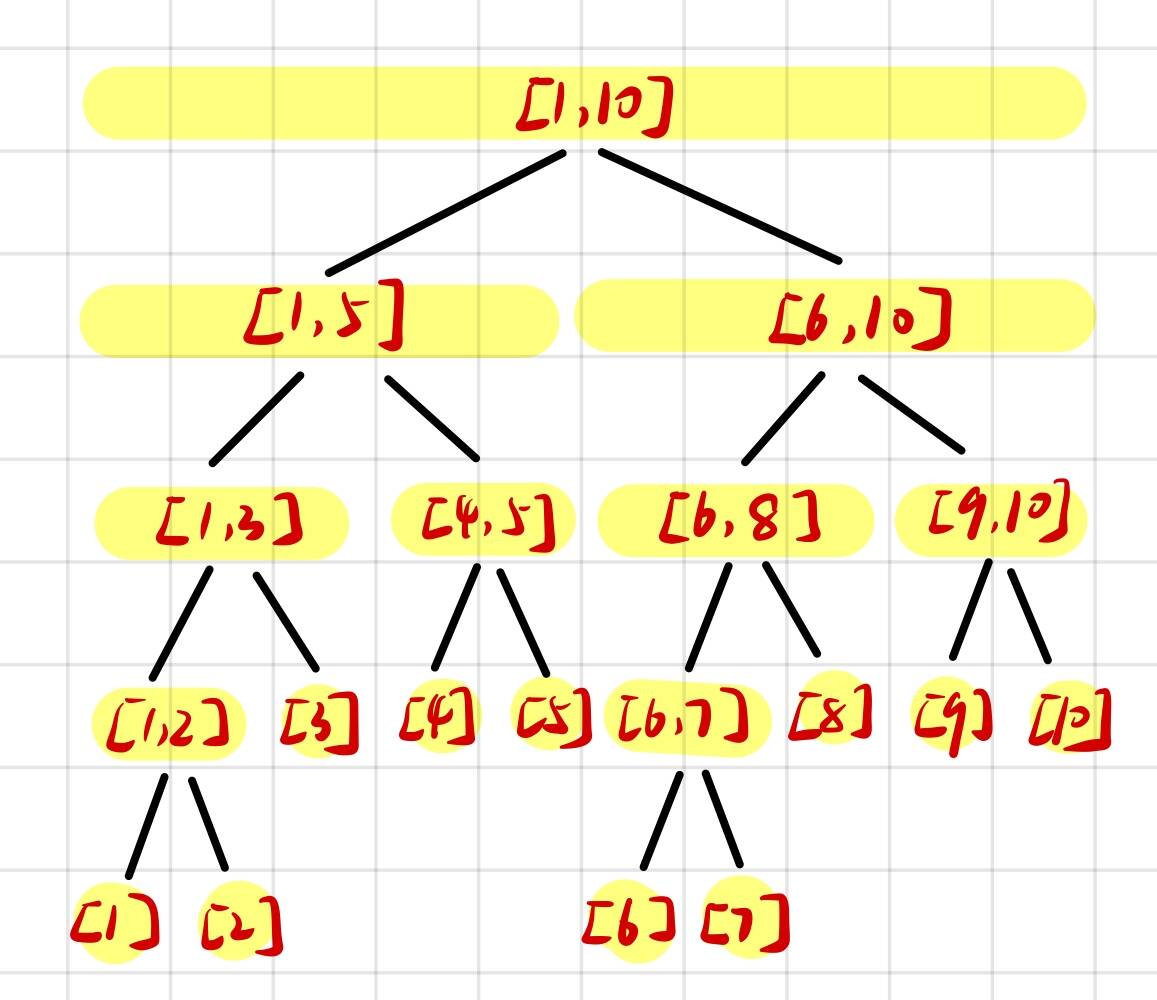
其中每一个节点里存的都是该节点管辖区间内（黄色区域）的最小值，图中共有 \(2n-1 = 19\) 个节点

build (静态开点)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct segment_tree
{
    int l,r;
    int val;
}t[4 * N];

void build(int u, int l, int r)
{
    t[u] = {l, r};
    if(l == r) return;  // 如果做赋初值等操作，要在最后pushup
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    // pushup(u)
}

query

设 \([L,R]\) 是要查询的区间，\([l,r]\) 是线段树的节点区间，\(s_l\) 为 \([l,r]\) 的左儿子区间，\(s_r\) 为区间 \([l,r]\) 的右儿子区间 1. \([l,r] \in [L,R]\) ，直接返回 \([l,r]\) 节点存的值 2. \([L,R] \cap s_l \neq \varnothing\) ，递归处理左儿子 3. \([L,R] \cap s_r \neq \varnothing\) ，递归处理右儿子

例如对上图线段树查询区间 \([5，9]\) 的最小值的情况如下：

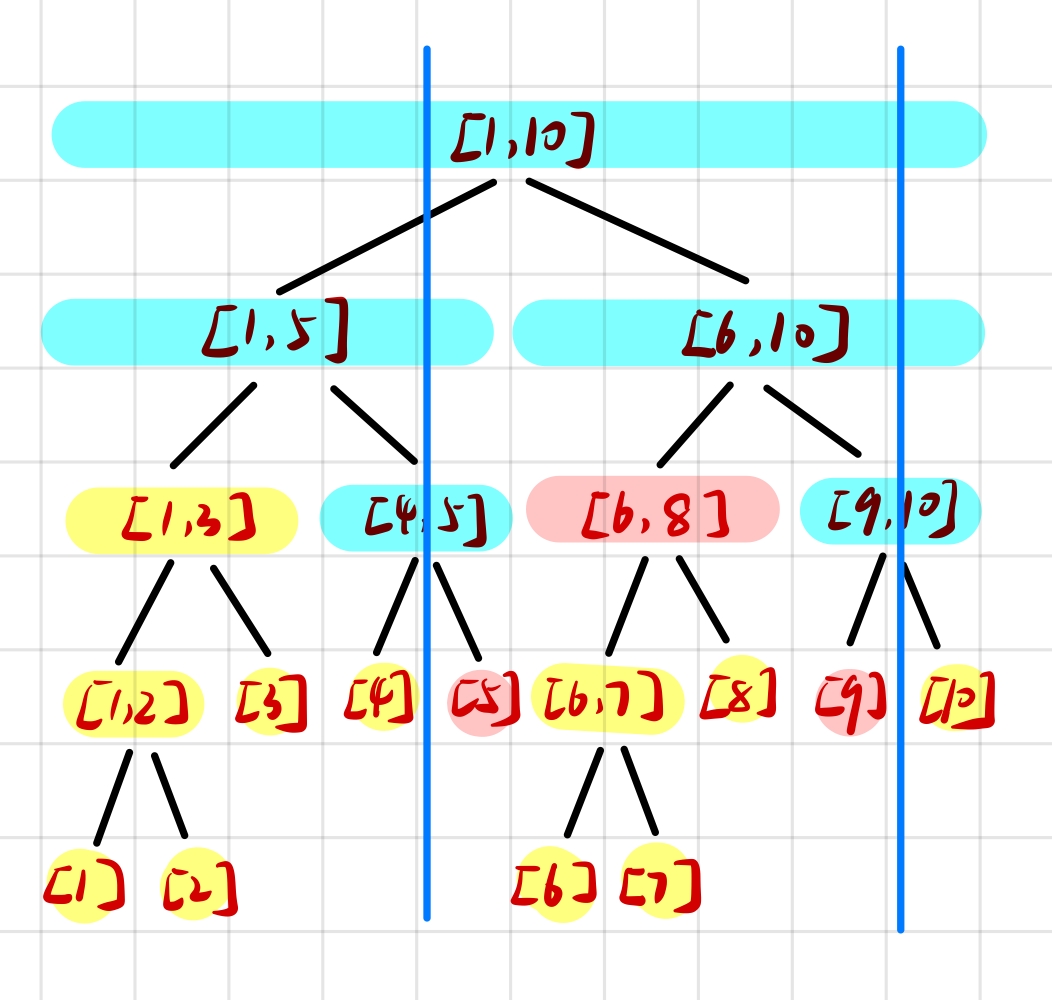
其中，蓝色区间是进行了递归查询左/右儿子的区间，红色区间是直接可以获取到值的区间，黄色是没有被访问到的区间

时间复杂度约 \(O(4log n)\) 

1
2
3
4
5
6
7
8
9
int query(int u, int l, int r)
{
    if(l <= t[u].l && t[u].r <= r) return t[u].val;
    int mid = t[u].l + t[u].r >> 1;
    int ans = 0;
    if(l <= mid) ans = query(u << 1, l, r);
    if(r > mid) ans = max(ans, query(u << 1 | 1, l, r));
    return ans;
}

pushup

用子节点的信息更新父节点的信息 

1
2
3
4
5
void pushup(int u)
{
    t[u].val = max(t[u << 1].val, t[u << 1 | 1].val);
    // 也可以采用重载 + 运算符
}

modify

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void modify(int u, int x, int d)
{
    // if(l <= t[u].l && t[u].r <= r) // 区间修改
    if(t[u].l == x && t[u].r == x) // 单点修改
        t[u].val = d; 
    else
    {
        int mid = t[u].l + t[u].r >> 1;
        // if(mid >= l)
        if(mid >= x) modify(u << 1, x, d);
        else modify(u << 1 | 1, x, d);
        pushup(u);
    }
}

以下讲解待补充（

线段树的可持久化（主席树）维护第 \(k\) 大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
const int N = 100010, M = 10010;

int n, m;
int a[N];
vector<int> nums;

struct Node
{
    int l, r;
    int cnt;    // 该数值区间内有多少个数
}tr[N * 4 + N * 17];

int root[N], idx;

int find(int x)
{
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}

// 动态开点
int build(int l, int r)
{
    int u = ++idx;
    if(l == r) return u;
    int mid = l + r >> 1;
    tr[u].l = build(l, mid);
    tr[u].r = build(mid + 1, r);
    return u;
}

int insert(int p, int l, int r, int x)
{
    int q = ++idx;  // 新版本的根节点
    tr[q] = tr[p];  // 将旧版本的数据复制到新版本
    if(l == r)
    {
        tr[q].cnt++;
        return q;
    }
    int mid = l + r >> 1;
    if(x <= mid)
        tr[q].l = insert(tr[p].l, l, mid, x);
    else
        tr[q].r = insert(tr[p].r, mid + 1, r, x);
    // pushup操作
    tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;
    return q;   // 返回根节点
}

// 二分做到了线段树里
int query(int q, int p, int l, int r, int k)
{
    if(l == r) return r;
    // 因为每个版本的节点都是一一对应的，类似前缀和的思想，可以直接相减
    // 得到 [l, r] 的数值区间内有多少个数
    int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
    int mid = l + r >> 1;
    if(k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
    else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> a[i];
        nums.push_back(a[i]);
    }

    // 离散化
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());

    root[0] = build(0, nums.size() - 1);    // 初始版本
    for(int i = 1; i <= n; i++)
    {
        int x = find(a[i]);
        // 第 i 个版本是在第 i - 1 个版本上进行添加的
        root[i] = insert(root[i - 1], 0, nums.size() - 1, x); 
    }
    while (m -- )
    {
        int l, r, k;
        cin >> l >> r >> k;
        int pos = query(root[r], root[l - 1], 0, nums.size() - 1, k);
        cout << nums[pos] << "\n";
    }

    return 0;
}

Lazy Tag

维护序列

区间加、区间乘，问区间和 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
typedef long long ll;
const int N = 1e5 + 2;
int p, n;
struct node {
    int l, r;
    ll sum;
    ll add = 0, mul = 1;
}t[N * 4];
int a[N];
void pushup(int u)
{
    t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
    t[u].sum %= p;
}

void build(int u, int l, int r)
{
    if (l == r)
    {
        t[u] = {l, r, a[r], 0, 1};
        //printf("build : t[%d].sum = %lld\n", u, t[u].sum);
        return;
    }
    int mid = l + r >> 1;
    t[u] = { l,r };
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

// 统一操作，先乘再加！！！！
void calculate(node& t, ll add, ll mul) // 多次操作写成一个函数简洁一些，记得加引用QAQ！！！
{
    t.mul  = (t.mul * mul)%p;   // 多取模（）
    t.add = (t.add * mul + add)%p;
    t.sum = (t.sum * mul + (t.r- t.l + 1)*add)%p;
}

// 将父节点的信息更新给子节点，同时清除父节点上的 tag 标记
void pushdown(int u)
{
    calculate(t[u<<1],t[u].add,t[u].mul);
    calculate(t[u<<1|1],t[u].add, t[u].mul);
    t[u].add = 0;
    t[u].mul = 1;

}


void modify(int u, int l, int r, int c,int d)
{
      if(t[u].l >= l && t[u].r <= r)
      {
        calculate(t[u],d,c);
        return;
      }
      // 分裂修改时一定要先 pushdown
      pushdown(u);
      int mid = t[u].l + t[u].r >>1;
      if(mid >= l)modify(u << 1, l, r, c, d);
      if(mid < r)modify(u << 1 | 1, l, r, c, d);
      pushup(u);

}

ll ask(int u, int l, int r)
{
    if (t[u].l >= l && t[u].r <= r)
    {
        //printf("t[%d].sum = %lld\n",u,t[u].sum);
        return t[u].sum;
    }
    pushdown(u);
    ll ans = 0;
    if (t[u << 1].r >= l)ans = ask(u << 1, l, r);
    ans %= p;
    if (t[u << 1 | 1].l <= r)ans += ask(u << 1 | 1, l, r);
    ans %= p;
    return ans;
}

int main()
{
    cin >> n >> p;
    for (int i = 1; i <= n; i++)cin >> a[i];
    build(1, 1, n);
    int m;cin >> m;
    int op, l, r, d;
    while (m--)
    {
        cin >> op >> l >> r;
        if (op != 3)
        {
            cin >> d;
            if(op == 1)
                modify(1, l, r, d, 0);
            else
                modify(1, l, r, 1, d);
        }
        else {
            cout << ask(1, l, r) << '\n';
        }
    }
    return 0;
}

线段树合并

技能树待点亮（