图论

Posted on Edited on Views:

邻接表

建无向图的时候，add(a,b), add(b,a) ，所以每条边都是成对的，即编号 \((0,1)、(2,3)、(4,5) \dots\) 是一组 （正向边，反向边）, 所以如果 \(i\) 是正向边，那么它的反向边就是 \(i \oplus 1\)

1
2
3
4
5
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

最短路

参考oiwiki

传递闭包

若 \(a \rightarrow b \rightarrow c\) 则连接一条 \(a \rightarrow c\) 的边，即：将所有间接可以到达的点，都用一条直接的边相连起来 

1
2
3
4
5
6
7
void floyd()
{
    for(int k = 0; k < n; k ++)
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                d[i][j] |= d[i][k] && d[k][j];
}

1
2
3
4
5
6
7
8
9
10
11
int a, b;
cin >> a >> b;
d[a][b] = 1;
for(int x = 0; x < n; x++)
{
    if(d[x][a]) d[x][b] = 1;
    if(d[b][x]) d[a][x] = 1;
    for(int y = 0; y < n; y++)
        if(d[x][a] && d[b][y]) d[x][y] = 1;
}

最小生成树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
long long kruskal()
{
    sort(edge.begin(), edge.end());
    for(int i = 1; i <= n; i++) p[i] = i;
    long long sum = 0;
    for(int i = 0; i < edge.size(); i++)
    {
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;
        int ra = find(a), rb = find(b);
        if(ra != rb)
        {
            p[ra] = rb;
            edge[i].is = true;
            sum += w;
        }
    }
    return sum;
}

负环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool spfa()
{
    memset(dist, 0, sizeof dist);
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    queue<int> q;
    for(int i = 1; i <= n; i++) q.push(i), st[i] = true;
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n) return true;
                if(!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    
    return false;
}

差分约束

最短路的松弛操作： 

1
2
if(dist[j] > dist[t] + w[i])
    dist[j] = dist[t] + w[i];
所以，当求解完最短路后，设 \(A(i,j)\) ：点 \(i\) 和 点 \(j\) 之间有一条从 \(i\) 指向 \(j\) 的有向边，则满足：\((\forall i) (\forall j)(A(j, i) \rightarrow (dist[i] \le dist[j] + w[j][i]))\)

对于一组不等式： \(x_i \le x_j + c_k\) 其中 \(c\) 是常数，若我们对每一个不等式都从点 \(x_j\) 向点 \(x_i\) 连一条长度为 \(c\) 的有向边（注意方向是从 \(j\) 到 \(i\) ，说明从 \(j\) 可以走到 \(i\) ，即 \(dist[i]\) 可以有可能被 \(dist[j]\) 更新），则跑完最短路之后的 \(dist\) 数组就是原不等式组的一个可行解，无解的情况即有负环存在

证明负环无解

差分约束

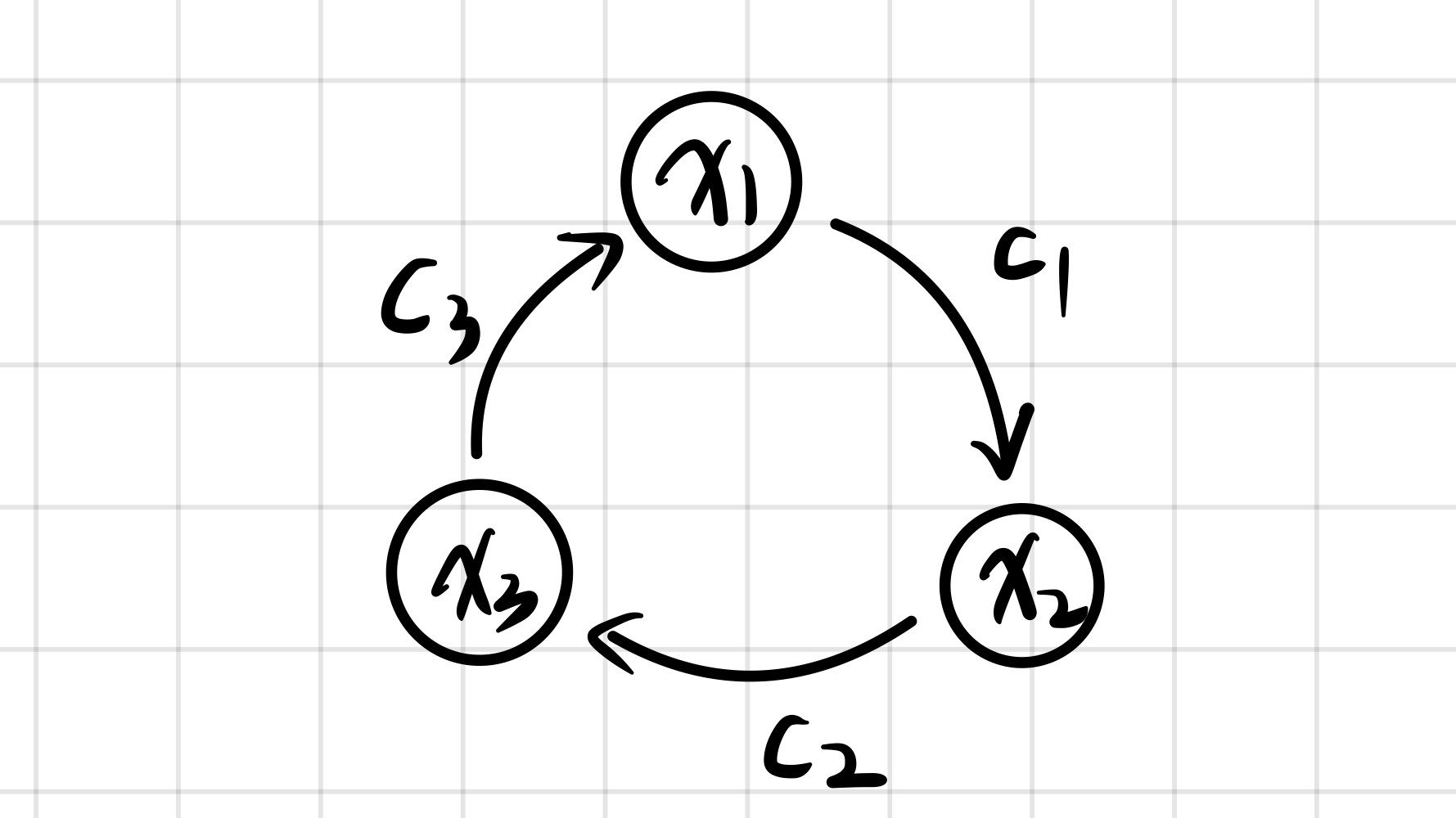
如上图我们建立的不等式关系为： \[ \begin{align} x_2 &\le x_1 + c_1 \nonumber \\ x_3 &\le x_2 + c_2 \nonumber \\ x_1 &\le x_3 + c_3 \nonumber \\ \end{align} \] 我们可以进行一个放缩： \[ \begin{align} x_1 &\le x_3 + c_3 \nonumber \\ &\le x_2 + c_2 + c_3 \nonumber \\ &\le x_1 + c_1 + c_2 + c_3 \nonumber \end{align} \] 由于是负环，所以 \(c_1 + c_2 + c_3 < 0\)，则上述不等式说明 \(x_1\) 小于自己加上一个负数，这是显然矛盾的

求最值

若我们要求解这组不等式的每一个变量 \(x\) 的最值，则必有一个约束条件形如：\(x \ge 0\)，否则所有等式都是相对关系，我们可以在等式两边同时加上一个常数 \(d\) 来获得新的解，此时变量 \(x\) 的值域可从负无穷到正无穷，无法求出最值

处理形如 \(x_i \le c\) 其中 \(c\) 是一个常数：建立一个源点，假设这个点为 \(0\) 号点，则从 \(x_0\) 向 \(x_i\) 连一条长度为 \(c\) 的有向边，其中 \(x_0 = 0\) 即 \(dist[0] = 0\)

最大值

由于存在最值，我们一定可以将 \(x_i \le x_j + c_i\) 通过如 \(x_i \le x_k + c_j + c_i\) 这样的放缩，放缩到 \(x_i \le x_0 + c_0 \dots + c_i\)，由于 \(x_0 = 0\)，所以此放缩后的不等式等价于从 \(0\) 号点走到 \(i\) 的所有路径，而我们要求的最大值（\(x_i\) 的上界）就是所有路径长度中的最小值，也即从 \(0\) 号点到 \(i\) 的最短路

最小值

与最大值类似，\(x_j \ge x_i + c_i\)，我们最后可以放缩得到 \(x_j \ge x_0 + c_0 \dots +c_i\)，此不等式等价于所有从 \(0\) 号点走到 \(j\) 号点的路径长度，而我们要求的最小值（\(x_j\)的下界），就是所有路径长度中的最大值，也即从 \(0\) 号点到 \(j\) 的最长路

做法总结

以最长路为例： 1. 边权无限制：\(\text{spfa} \ \ \ O(nm)\) 2. 边权非负：\(\text{tarjan} \ \ \ O(n + m)\) 3. 边权 \(> 0\) : 拓扑排序 \(O(n + m)\)

连通分量

一些定义

  1. 对于一个有向图，连通分量指：对于分量中的任意两点 \(u, v\)，必然可以从 \(u\) 走到 \(v\)， 且从 \(v\) 走到 \(u\)

  2. 强连通分量（SCC）：极大连通分量

  3. 桥：对于一个连通图来说，如果把某条边删掉之后，会使得原来的整个连通图变得不连通，这个边就称作桥
    等价地说，一条边是一座桥当且仅当这条边不在任何环上

  4. 边双连通分量（e - DCC）：极大的，不含有桥的连通分量
    性质：任意两点之间含有两条不相交的路径

  5. 割点：对于一个连通图，如果把某个点删掉（）会删除与其关联的所有边）之后，整个图会变得不连通，那么这个点就称为割点
    每个割点：至少属于两个连通分量

  6. 点双连通分量（v - DCC）：极大的，不含有割点的连通分量

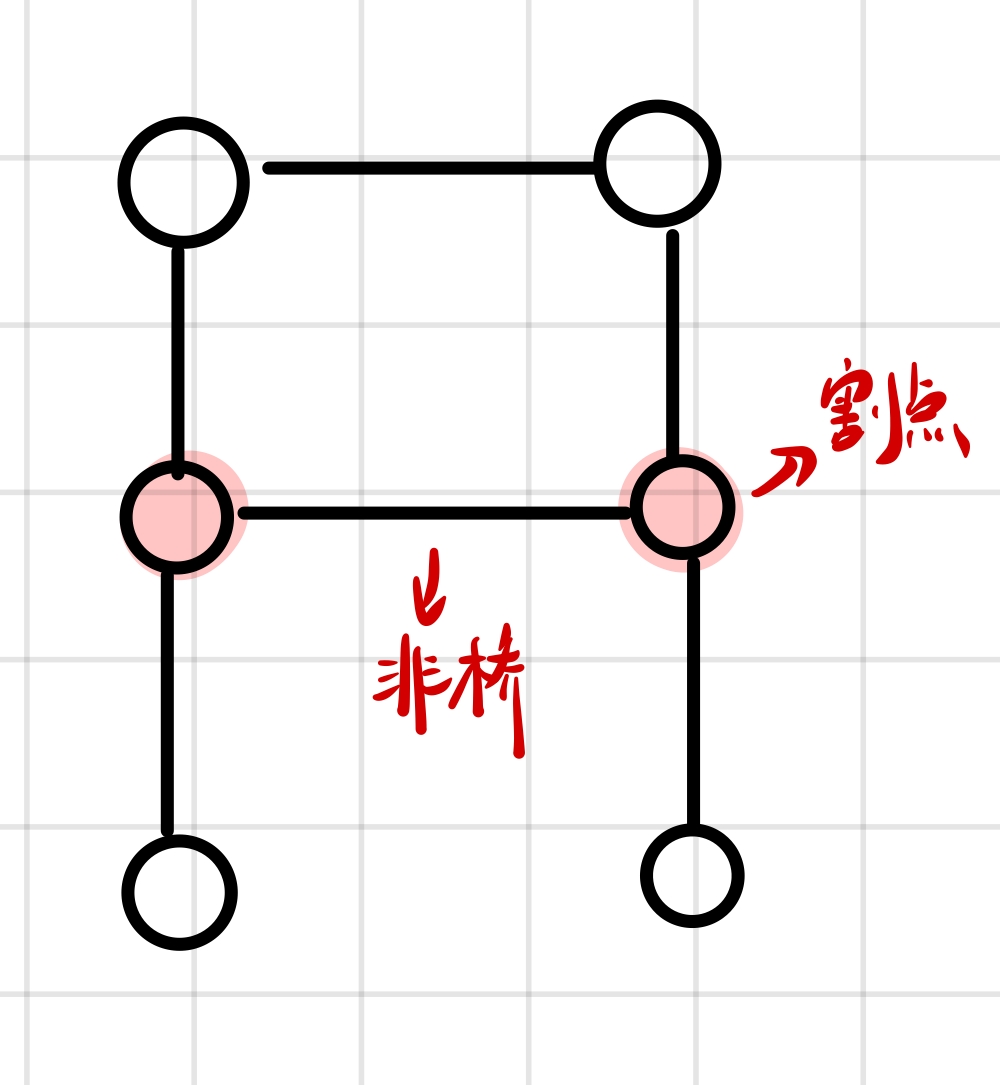
  7. 两个割点之间的边不一定是桥：

    割点和桥

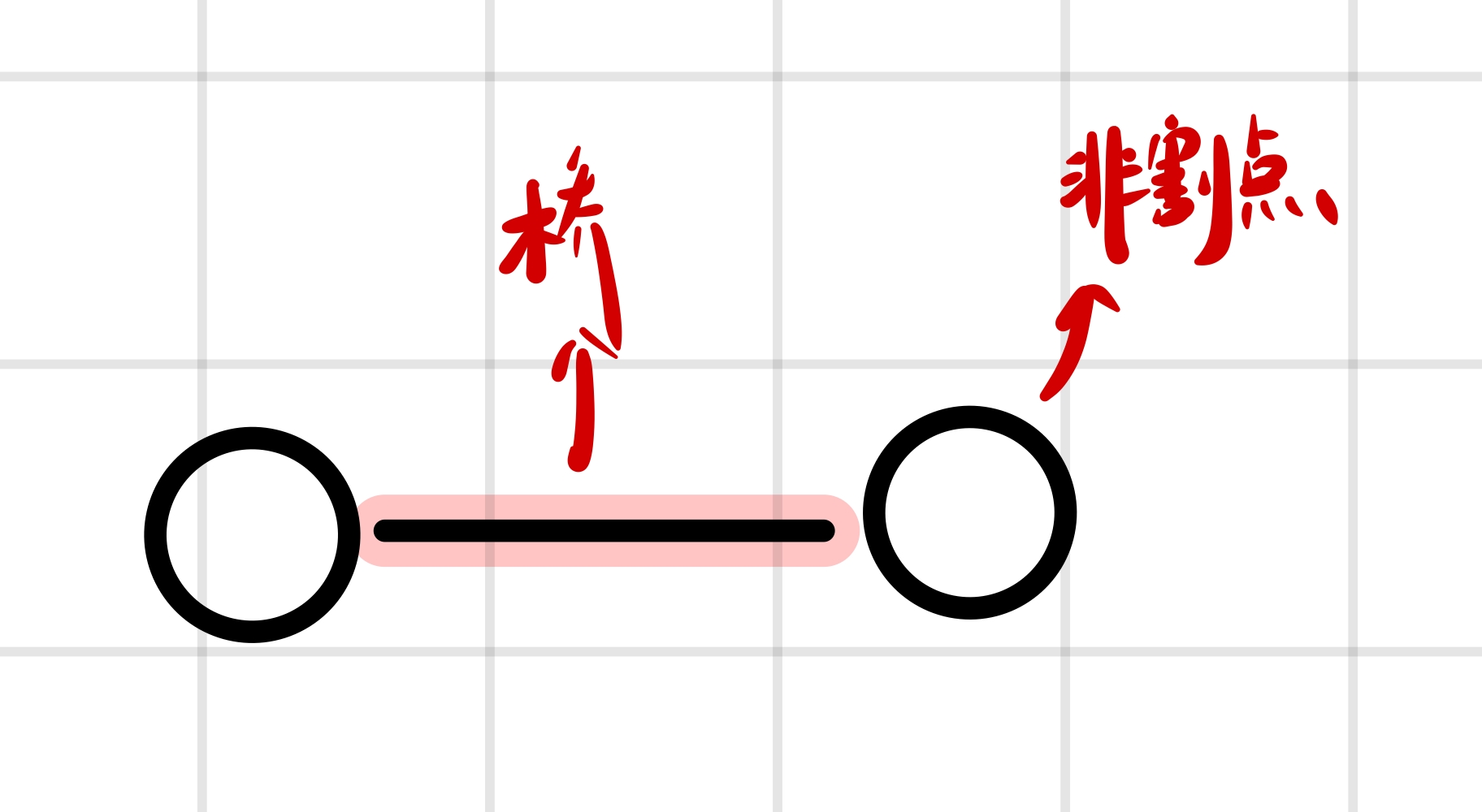
    一个桥的两个端点不一定是割点（一个点连通分量不一定是边连通分量）：

    桥和割点

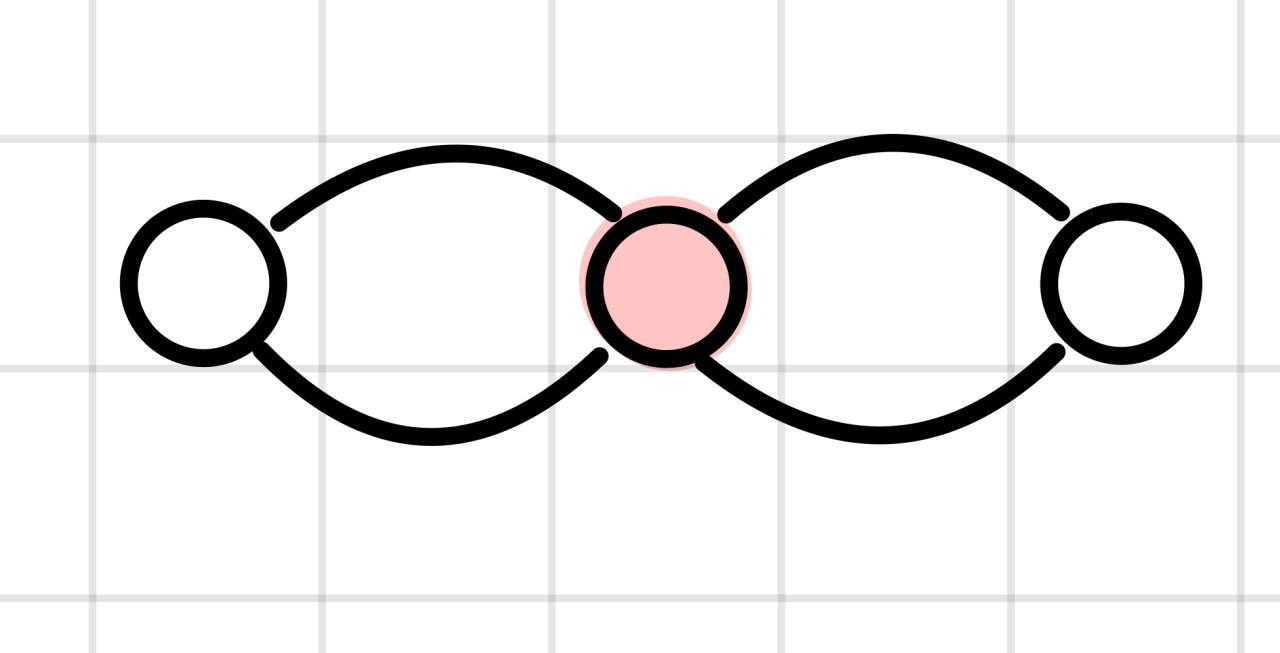
    一个边连通分量不一定是点连通分量：

    边连通分量和点连通分量

一些结论

  1. 将有向图变成强连通分量所需要加的最少边数为 \(\max(p, q)\)，其中 \(p\) 是缩点之后入读为 \(0\) 的点的数量， \(q\) 是缩点之后出度为 \(0\) 的点的数量
  2. 将无向图连通图变成边双连通分量所需要加的最少边数是 \(\lceil cnt / 2 \rceil\)，其中 \(cnt\) 是缩点之后叶子节点的数量

有向图的强连通分量

有可能可以将强连通分量缩点之后，变成一个拓扑图进行递推

\(\text{Tarjan}\) 求 \(\text{SCC}\) :

在 DFS 的过程中：树枝边，前向边，后向边，横叉边

如果 \(x\) 在强连通分量中：1. 存在后向边指向祖先节点 2. 先走到横叉边，横叉边再走到祖先节点

对每个点定义两个时间戳：\(\text{dfn}[u]\) 表示遍历到 \(u\) 的时间戳，\(\text{low}[u]\) 表示从 \(u\) 开始走，所能遍历到的最小时间戳
\(u\) 是其所在强连通分量的最高点 \(\iff \text{dfn}[u] == \text{low}[u]\)

代码中的 else if (in_stk[j]) low[u] = min(low[u], dfn[j]); 可以改为 else if (in_stk[j]) low[u] = min(low[u], low[j]);

原因（？

else if 那一行里面能不能把 dfn[j] 换成 low[j] 呢？显然是可以的，
这一行只会在压缩点的过程中用到，因为非压缩点是按照拓扑序遍历的，拓扑序不会遍历到之前搜到的点，否则就成环了。 在压缩的过程中我们也只会在拆环的时候（即遍历到一个环的起点的时候）才会用到这一行，如果是原代码那么返回路径上存的就是起点的实际编号值dfn，
如果改成 low 呢？只有从起点已经遍历过一个环了，并且终点在起点前面，那么 low 就是存的前面起点的值，即我们刚遍历大环成为一个相对的小环了，这时候存的此时起点能走到的最小值
会不会改了之后成为一个较大值呢？不会，因为low是通过两次min函数比较出来的，最起码比自己的编号值要小，不然也不会完成赋值。

我们可以讨论一下两种写法的意义何在呢？
第一种模板的写法将拆环的起点编号dfn存到每一个点的 low 里面去了，因为 dfn 编号是不参与比较与赋值的锚定顺寻的编号，所以我们可以知道每一点第一次拆环的时候是从哪个起点上面拆下来的
改成 low 之后我们就只能知道每一个点第一次拆环的时候在环上面能追溯到最前面的环起点是哪一个值

作者：BT7274 链接：https://www.acwing.com/file_system/file/content/whole/index/content/5627037/ 来源：AcWing 著作权归作者所有

缩点：从每个点出发遍历邻边，如果这条边的两个点属于不同的强连通分量，就加一条边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u, in_stk[u] = true;
    
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do {
            y = stk[top -- ];
            in_stk[y] = false;
            id[y] = scc_cnt;
        } while (y != u);
    }
}

无向图的边双连通分量

如何找到所有桥：设当前在搜的节点是 \(x\)，向下再搜一条边到节点 \(y\)，若 \(y\) 可以走到 \(x\) 或者 \(x\) 的祖先节点，那么这条 \(x——y\) 的边就不是桥，否则 \(y\) 最早只能走到 \(y\) 自己，那么这条边就是桥，因此，是桥 \(\iff \text{dfn}[x] < \text{low}[y]\)

如何找到所有的边双连通分量：若 \(\text{dfn}[x] == \text{low}[x]\)，则说明，\(x\) 向上的那条边是桥，则当前在栈中的，\(x\) 的子树节点，就是一个边双连通分量

为什么这里不用记录是否在栈中：可能是因为无向图在搜的时候没有横向边，\(u\) 不会搜到已经在其他边双连通分量的点了，所以只要是 \(u\) 可以走到的点，就能用来更新 \(\text{low}[u]\)

同一个边双连通分量中的点的 low 标记不一定都相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;
    
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j])
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if (i != (from ^ 1))
            low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u])
    {
        ++ dcc_cnt;
        int y;
        do {
            y = stk[top -- ];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

无向图的点双连通分量

如何求割点：从点 \(x\) 向下再搜一条边到点 \(y\)，若 \(y\) 不可以走到 \(x\) 的祖先节点： 1. \(x\) 不是根节点，那么 \(x\) 是割点 2. 如果 \(x\) 是根节点，则如果有至少两个 \(y_i\) 满足 \(\text{low}[y_i] \ge \text{dfn}[x]\)，则 \(x\) 是割点

缩点： 1. 每个割点单独作为一个点 2. 从每个 v-DCC 向其所包含的每个割点连一条边 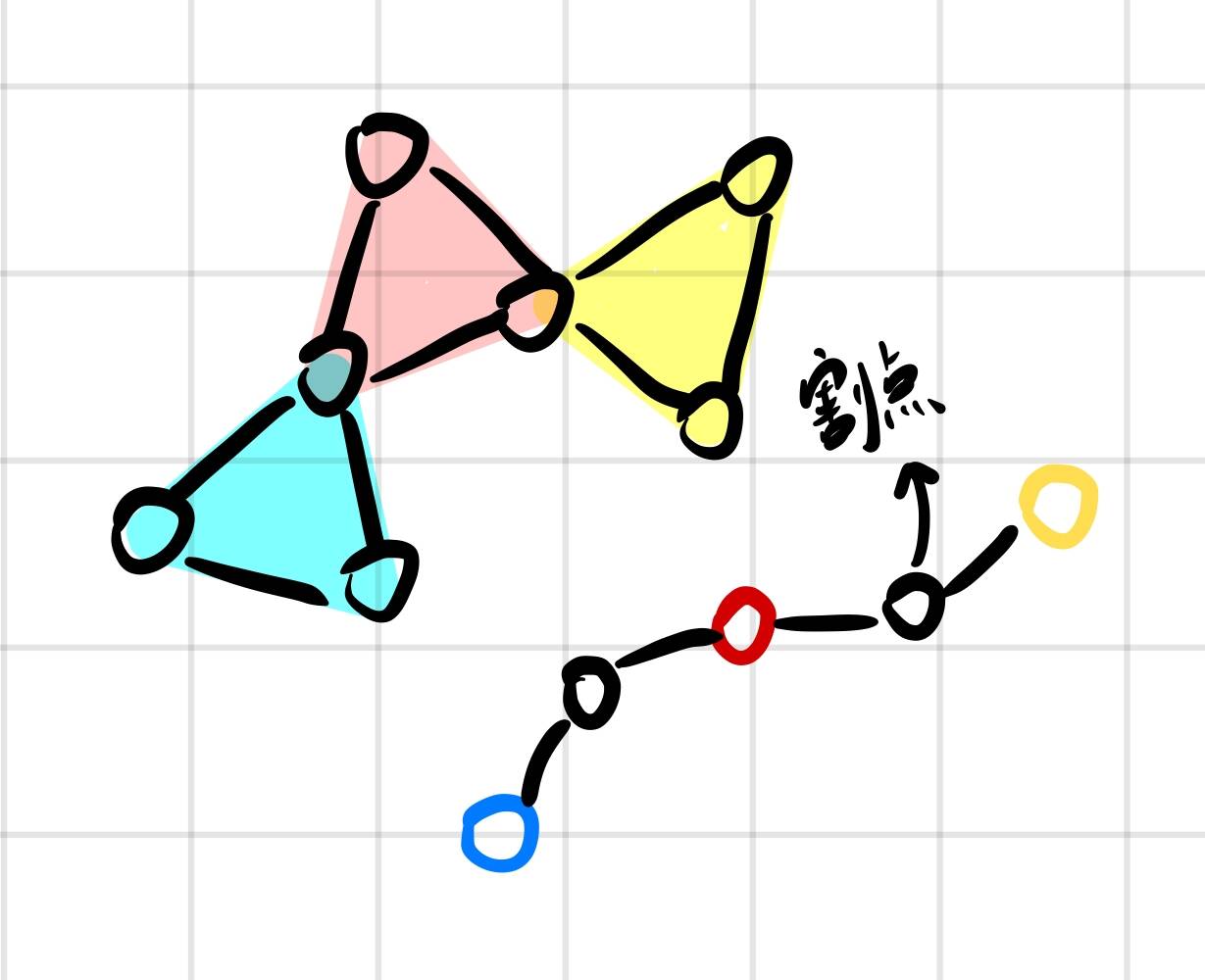点缩点

对于缩点之后的节点，每个节点（除了割点之外）的度数就代表它所代表的 v-DCC 中有几个割点

else low[u] = min(low[u], dfn[j]); 中不可以将 dfn[j] 换成 low[j]
原因：会使得无法找到某些割点 >对于求割点来说，我们考虑的是删掉这个点之后的剩余部分还能不能联通，如果此时我们采用这种更新方式，可能就会存在某个点，它更新后反而能回到我们考虑的点的上方（通过间接方式），根据我们对割点的判断low[x] <= low[y], 我们会发现此时x居然不被判定为割点了。原因就在于，我们在间接去到S的时候，没有考虑到，割点会删掉x，这样子我们根本没法越过x去s

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;
    //u是孤立点：u是根节点且没有邻边
    if (u == root && h[u] == -1)
    {
        dcc_cnt ++ ;
        dcc[dcc_cnt].push_back(u);
        return;
    }
    
    int cnt = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (dfn[u] <= low[j])
            {
                cnt ++ ;
                if (u != root || cnt > 1) cut[u] = true;    //u是割点
                ++ dcc_cnt;
                int y;
                do {
                    y = stk[top -- ];
                    dcc[dcc_cnt].push_back(y);
                } while (y != j);
                dcc[dcc_cnt].push_back(u);
            }
        }
        else low[u] = min(low[u], dfn[j]);
    }
}

1
2
for(int root = 1; root <= n; root++)
    if(!dfn[root]) tarjan(root);
1
2
3
4
5
6
7
//求每个 v-DCC 的割点数量（度数）
for(int i = 1; i <= dcc_cnt; i++)
{
    int cnt = 0;
    for(int j = 0; j < dcc[i].size(); j++)
        if(cut[dcc[i][j]]) cnt++
}

LCA

倍增LCA

\(\text{fa}[i,j]\) 表示从 \(i\) 开始， 向上跳 \(2^j\) 步所到达的点 哨兵：如果从 \(i\) 开始跳 \(2^j\) 步会跳过根节点，那么 \(\text{fa}[i,j] = 0, depth[0] = 0\)

  1. 先将两个点跳到同一层
  2. 如果没有跳到同一个点，就让两个点同时往上跳，一直跳到它们的最近公共祖先的下一层

预处理 \(O(n \log n)\)
查询 \(O(\log n )\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void bfs(int root)  // 预处理倍增数组
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;  // depth存储节点所在层数
    int hh = 0, tt = 0;
    q[0] = root;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q[ ++ tt] = j;
                fa[j][0] = t;  // j的第二次幂个父节点
                for (int k = 1; k <= 15; k ++ )
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
            }
        }
    }
}

int lca(int a, int b)  // 返回a和b的最近公共祖先
{
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    if (a == b) return a;
    for (int k = 15; k >= 0; k -- )
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    return fa[a][0];
}

离线LCA， \(O(n + m)\)

以询问树中两个点的最小距离为例： 在深度优先遍历时，将所有点分成三大类： 1. 已经遍历过，且回溯过的点，状态标记为 \(2\) 2. 正在搜索的分支，状态标记为 \(1\) 3. 还未搜索到的点，状态标记为 \(0\)

对于当前正在搜索的点 \(x\)，去找一下所有与这个点相关的询问，如问 \(x\) 和点 \(y\) 的最近公共祖先是谁，如果点 \(y\) 的状态是 \(2\)，那么它们的最近公共祖先就是 \(\text{find}[y]\)

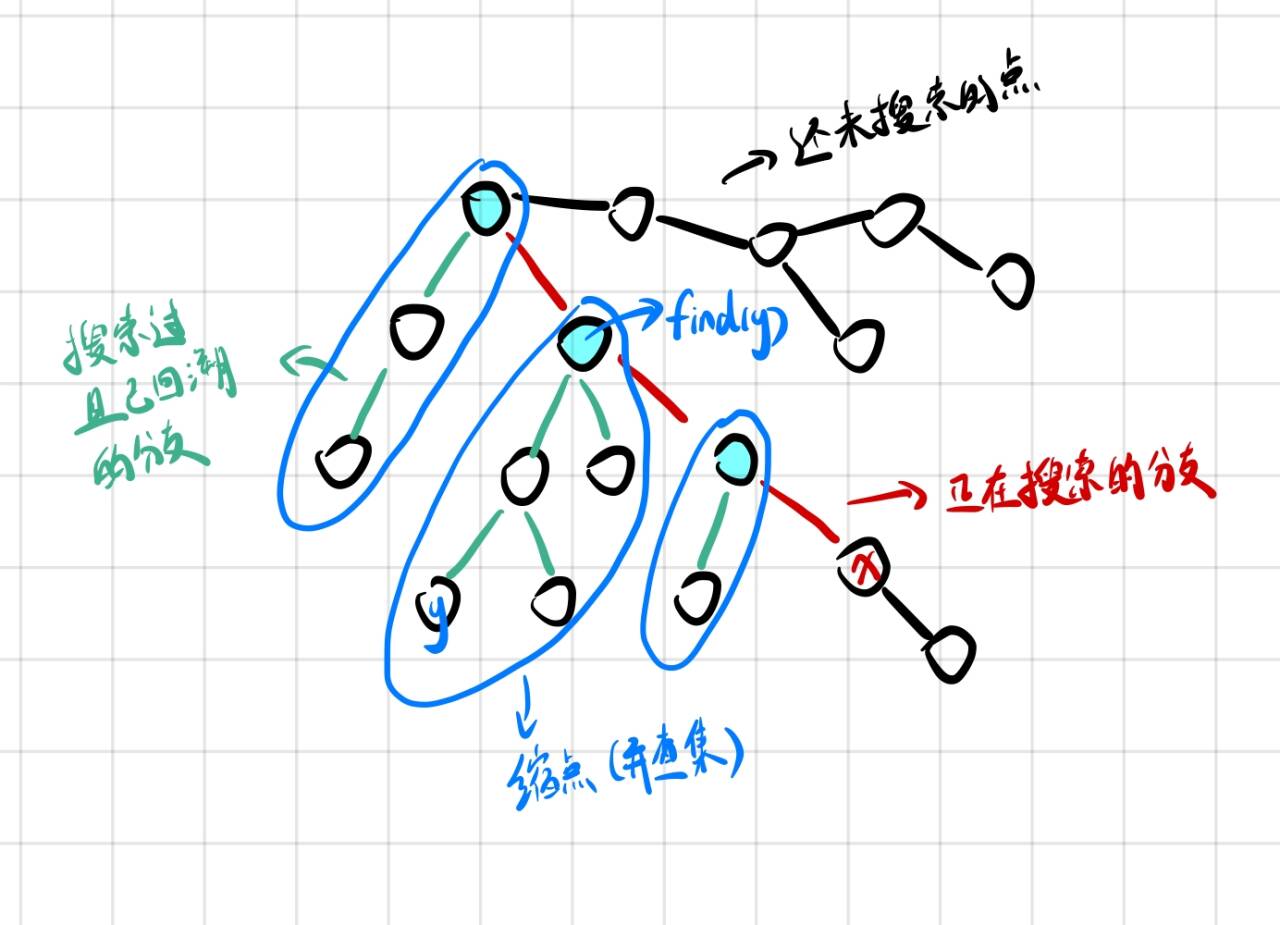
最近公共祖先 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
int p[N];
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int dist[N];
void dfs(int u, int fa) //预处理每个点到根节点的距离
{
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == fa) continue;
        dist[j] = dist[u] + w[i];
        dfs(j, u);
    }
}


int st[N];
int res[M];
void tarjan(int u)
{
    st[u] = 1;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            tarjan(j);
            p[j] = u;
        }
    }

    for(const auto& [a, b] : query[u])
    {
        if(st[a] == 2)
        {
            int r = find(a);
            //这两个点之间的距离等于它们各自到根节点的距离之和
            //减去2倍的它们的最近公共祖先到根节点的距离
            res[b] = dist[u] + dist[a] - dist[r] * 2;
        }
    }

    st[u] = 2;
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < n - 1; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    for(int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        if(a != b)
        {
            query[a].push_back({b, i});
            query[b].push_back({a, i});
        }
    }

    for(int i = 1; i <= n; i++) p[i] = i;

    dfs(1, -1);

    tarjan(1);

    for(int i = 0; i < m; i++) cout << res[i] << '\n';

}

二分图

前置术语

  1. 最大匹配：选出最多的边数，使得任意两条边都没有公共点

  2. 增广路径：从一个非匹配点出发，沿着非匹配边——匹配边——非匹配边——匹配边 \(\dots\) 交替走，若最后能走到另一个非匹配点，则称这条路径为增广路径

  3. 最大匹配 \(\iff\) 不存在增广路径，因为如果存在增广路径，我们可以将路径上的所有匹配边变成非匹配边，非匹配边变成匹配边，此时匹配数量就增加 \(1\) 了

  4. 最小点覆盖：选出最少的点数使得可以覆盖所有边

  5. 最大独立集：选出最多的点，使得选出的内部点之间没有边

  6. 最大团（最大独立集的补图）：选出最多的点，使得选出的内部点，任意两点之间都有边

  7. 最小路径点覆盖：对于一个DAG（有向无环图），用最少的互不相交的路径将所有点覆盖

  8. 最小路径重复点覆盖：与最小路径点覆盖不同的是：路径可以相交

二分图

  1. 二分图：可以将一个图的点分成两个集合，使得图中的所有边都在这两个集合之间，集合内部没有边
  2. 一个图是二分图 \(\iff\) 不存在奇数环 \(\iff\) 染色法不存在矛盾
  3. 对于 \(N \times M\) 的网格，我们将所有横纵坐标之和为偶数的染成黑色，横纵坐标之和为奇数的染成白色，在某些情况下可以看做是二分图
  4. 在二分图中，最小点覆盖 \(=\) 最大匹配数
    证明
    首先显而易见，最小点覆盖一定 \(\ge\) 最大匹配数，以下证明等于号成立：
    1. 求最大匹配
    2. 从左部每一个非匹配点出发做一遍增广路径标记所有经过的点
    3. 构造：选择左部所有未被标记的点和右部所有被标记的点

    证明：由于不存在增广路径，所以从左边的非匹配点出发一定不会走到右边的非匹配点，所以右边的所有非匹配点均未被标记

    由于从左边的非匹配点出发，所以左边的所有非匹配点均被标记

    在一条匹配边两端的点，要么同时被标记，要么同时不被标记，因为左边的匹配点只会从右边的匹配点走过来，所以左边的匹配点的标记状态和这条匹配边连接的右边的点的标记状态相同

    对于所有匹配边： 如果对应的匹配点被标记了我们选择右边的点，否则选择左边的点（保证了所有匹配边被选到了

    对于所有非匹配边（可以保证所有非匹配边都被选到：

    1. 左边的匹配点——右边的匹配点：若左边的匹配点被标记了，那么经过这条非匹配边，右边的匹配点也一定会被标记，由于右边的匹配点一定存在一条匹配边，且被标记了，所以我们会选择右边的点，若左边的匹配点没有被标记，同理我们会选到左边的点，即这条非匹配边一定会被选到
    1. 左边的匹配点——右边的非匹配点：我们可以知道右边的那个非匹配点一定没有被标记，若左边的匹配点被标记了，那么就一定可以从左边的这个匹配点走到右边的非匹配点，右边的点就会被标记，产生矛盾，所以左边的的匹配点也一定不会标记，对于左边的匹配点，一定会存在一条匹配边，由于没有被标记，我们选择了左边的点，所以所有从左边匹配点连接向右边非匹配点的边都会被选择到
    1. 左边的非匹配点——右边的匹配点：我们可以知道左边的那个非匹配点一定被标记，并且会从这个非匹配点出发经过右边的匹配点，所以右边的那个匹配点也一定被标记了，而右边的匹配点一定属于某一条匹配边，由于被标记了，那么右边的这个点就一定会被选择上，所以所有从左边非匹配点连向右边匹配点的边都会被选上
    1. 左边的非匹配点——右边的非匹配点：我们就可以添加一条新的匹配边了，与最大匹配矛盾，所以不存在这样的边
  5. 在二分图中，求最大独立集 \(\iff\) 去掉最少的点，将所有边都破坏掉 \(\iff\) 找最小点覆盖 \(\iff\) 找最大匹配，因此若总点数是 \(n\) ，最大匹配数是 \(m\) ，则最大独立集是 \(n - m\)
  6. 最小路径点覆盖：将所有点拆为两个点，分别为 \(i\) 和 \(i'\)，对于一条有向边 \((i,j)\) ,就连一条边从 \(i\) 到 \(j'\), 那么原图就可以变为二分图，在新图上求最大匹配就是最小路径点覆盖，但是在写代码的时候不用真的拆点（），\(d[i][j]\) 就可以表示是从 \(i\) 向 \(j'\) 的边
  7. 最小路径重复点覆盖：先对原图求一遍传递闭包，然后再在新图上求最小路径点覆盖，就是原图的最小路径重复点覆盖

匈牙利算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    
    return false;
}

欧拉路径/回路

  1. 无向图，所有边都是连通的
    1. 存在欧拉路径的充分必要条件：度数为奇数的点只能有 \(0\) 个或者 \(2\) 个
    2. 存在欧拉回路的充分必要条件：度数为奇数的点只能有 \(0\) 个
  2. 有向图，所有边都是连通的
    1. 存在欧拉路径的充分必要条件：所有点的出度均等于入度；或者除了两个点之外，其余所有点的出度等于入度，且剩余的两个点满足：一个点出度比入度多 \(1\) （起点），另一个点满足入度比出度多 \(1\) （终点）
    2. 存在欧拉回路的充分必要条件：所有点的出度均等于入度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int cnt = 0;
void dfs(int u)
{
    //注意这里是引用&
    for(int& i = h[u]; i != -1; i = ne[i])
    {
        if(used[i]) continue;
        used[i] = true;
        if(type == 1) used[i ^ 1] = true;

        int t;
        //对于无向图 (0,1)表示第一条边,(2,3)表示第二条边,所以要得到第t条边的编号 t = i/2 + 1;
        //对于有向图 (0) 表示第一条边,(1)表示第二条边 所以 t = i + 1;
        if(type == 1)   //type = 1是无向图，否则是有向图
        {
            t = i / 2 + 1;
            if(i & 1) t = -t;
        }
        else t = i + 1;

        int j = e[i];
        dfs(j);
        ans[++cnt] = t;
        if(i == -1) break; //有可能会越界（）
    }
}

//最后是倒着输出的
for(int i = cnt; i >= 1; i--)
        cout << ans[i] << " ";